Géométrie#
Nom, prénom:
Note:
| Question | 1 | 2 | 3 | 4 | 5 | 6 | Total |
|---|---|---|---|---|---|---|---|
| Points | 5 | 4 | 3 | 3 | 3 | 5 | 23 |
| Obtenus |
Détails des calculs obligatoires. Attention au soin. Calculatrice non autorisée.
Question 1 (5 pts)#
Répondez aux questions suivantes le plus précisément possible:
Complétez par le vocabulaire adéquat:
Les deux droites BC et DE sont parallèles.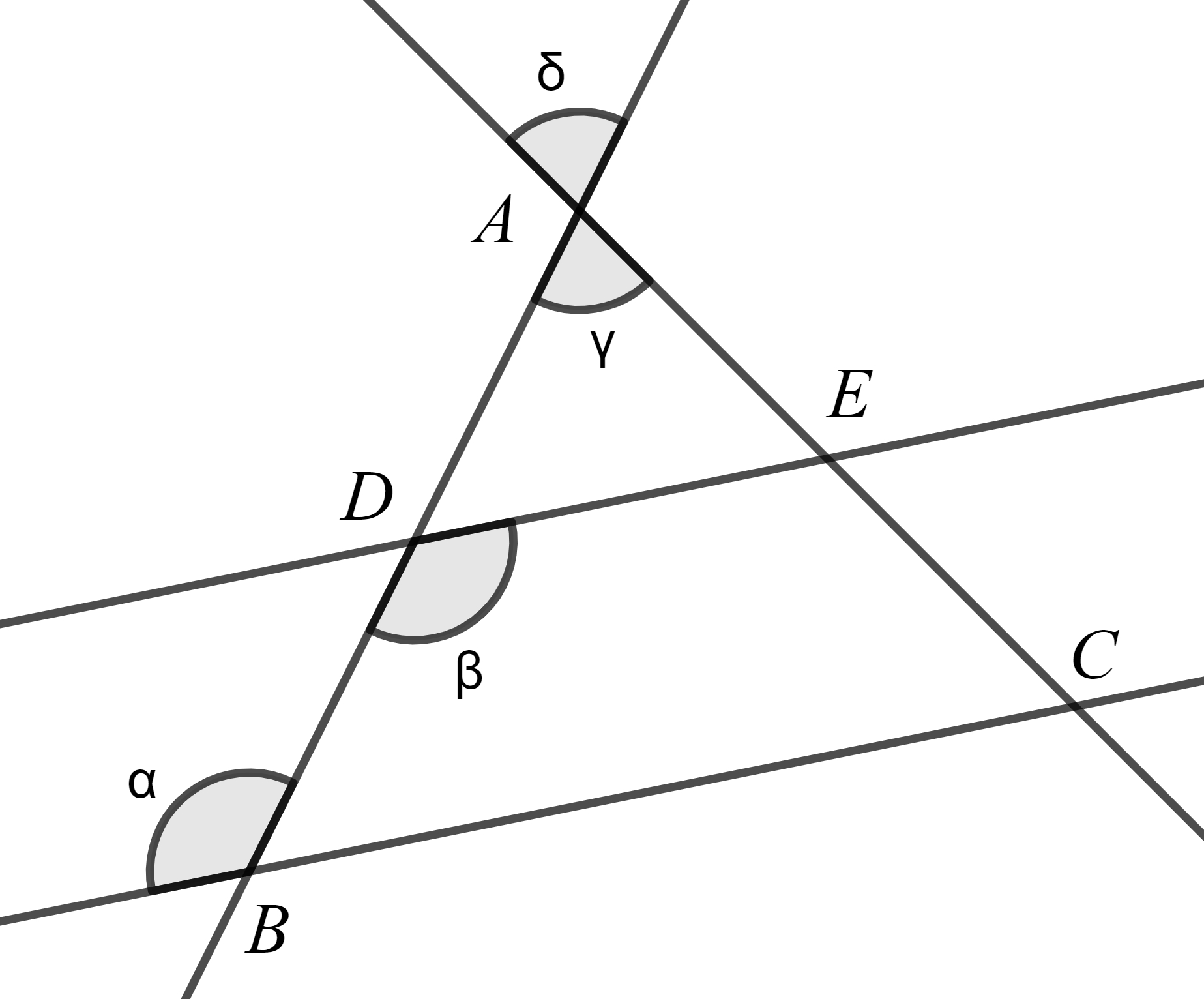
Les angles \(\alpha\) et \(\beta\) sont isométriques, car ils sont
Les angles \(\gamma\) et \(\delta\) sont isométriques, car ils sont
Énoncez le théorème de Thalès (les 3 rapports) en fonction de l'image ci-dessus.
Notez la définition générale des trois rapports trigonométriques.
Solution
alternes-internes / opposés par le sommet
\(\dfrac{\overline{AD}}{\overline{AB}}=\dfrac{\overline{AE}}{\overline{AC}}=\dfrac{\overline{DE}}{\overline{BC}}\) ou \(\dfrac{\overline{AB}}{\overline{AD}}=\dfrac{\overline{AC}}{\overline{AE}}=\dfrac{\overline{BC}}{\overline{DE}}\)
\(\sin(\dots) = \dfrac{\text{opp}}{\text{hyp}} \qquad\qquad\) \(\cos(\dots) = \dfrac{\text{adj}}{\text{hyp}} \qquad\qquad\) \(\tan(\dots) = \dfrac{\text{opp}}{\text{adj}}\)
Question 2 (4 pts)#
Soit le triangle \(ABC\) rectangle en \(A\) et \(\overline{AH}\) la hauteur.
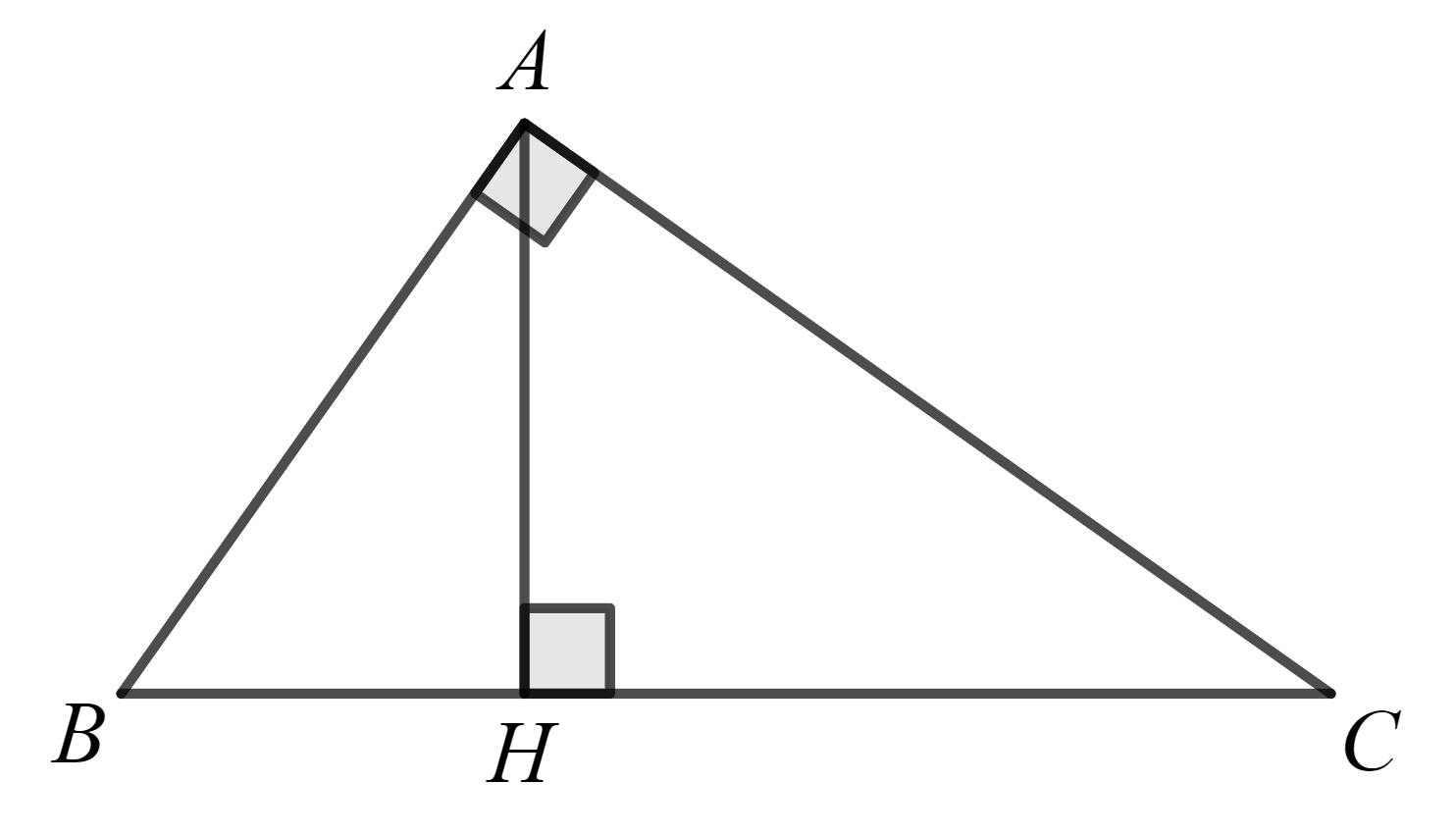
Énoncez le théorème de la hauteur en fonction du schéma ci-dessus.
Énoncez le théorème d'Euclide en fonction du schéma ci-dessus.
Sachant que \(\overline{BH} = 4\,cm\) et \(\overline{BC} = 8\,cm\), calculez \(\overline{AB}\).
Sachant que \(\overline{BH} = 2\,cm\) et \(\overline{AH} = 6\,cm\), calculez \(\overline{BC}\).
Solution
\(\overline{AH}^2 = \overline{BH} \cdot \overline{HC}\)
\(\overline{AB}^2 = \overline{BH} \cdot \overline{BC}\) et \(\overline{AC}^2 = \overline{HC} \cdot \overline{BC}\)
\(\overline{AB}^2 = \overline{BH} \cdot \overline{BC}\)
\[\begin{split}\overline{AB}^2 &= 4 \cdot 8\\ \overline{AB} &= \sqrt{32} = 5.7\,cm \end{split}\]\(\overline{AH}^2 = \overline{BH} \cdot \overline{HC}\)
\[\begin{split}6^2 &= 2 \cdot \overline{HC}\\ \overline{HC} &= \dfrac{36}{2} = 18\,cm\\ \overline{HC} &= 18 + 2 = 20 \,cm \end{split}\]
Question 3 (3 pts)#
Résolvez les deux triangles suivants, rectangles en \(A\), en complétant le tableau.
Notez tous les détails des calculs
\(a\) |
\(b\) |
\(c\) |
\(\beta\) |
\(\gamma\) |
|
|---|---|---|---|---|---|
a) |
\(49\,cm\) |
\(31\,cm\) |
... |
... |
... |
b) |
... |
... |
\(52\,cm\) |
\(39^\circ\) |
... |
Solution
\(a\) |
\(b\) |
\(c\) |
\(\beta\) |
\(\gamma\) |
|
|---|---|---|---|---|---|
a) |
\(49\,cm\) |
\(31\,cm\) |
\(37.9\,cm\) |
\(39.2^\circ\) |
\(50.8^\circ\) |
b) |
\(67\,cm\) |
\(42.1\,cm\) |
\(52\,cm\) |
\(39^\circ\) |
\(51^\circ\) |
Question 4 (3 pts)#
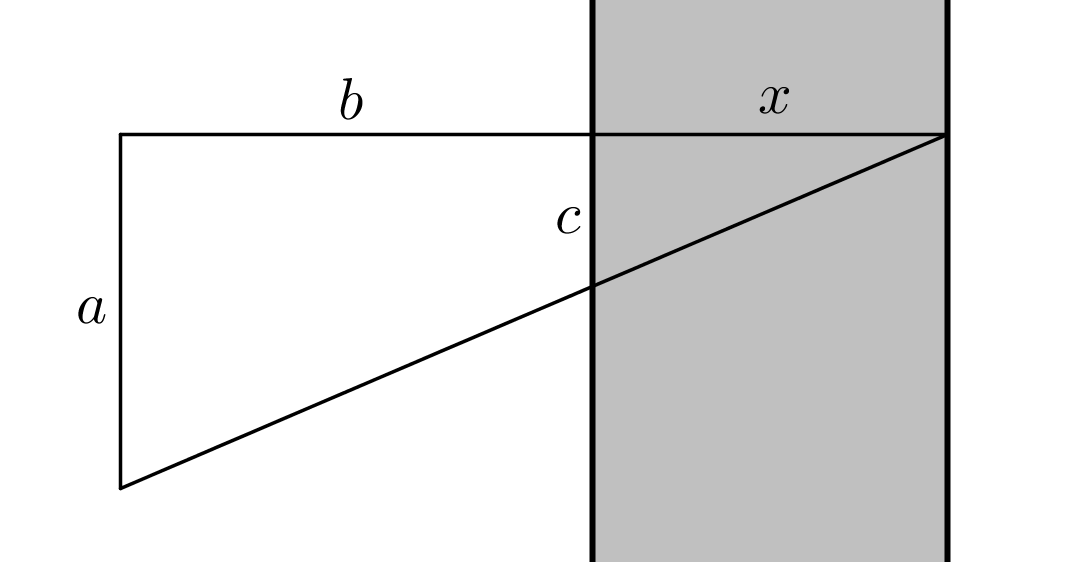
Pour déterminer la largeur \(x\) d'une rivière, nous pouvons utiliser la construction suivante et mesurer \(a\), \(b\) et \(c\).
Que vaut la largeur de la rivière si \(a=25\,m\), \(b=8\,m\), \(c=10\,m\)?
Solution
La largeur de la rivière vaut ~ 5.3 m.
Question 5 (3 pts)#
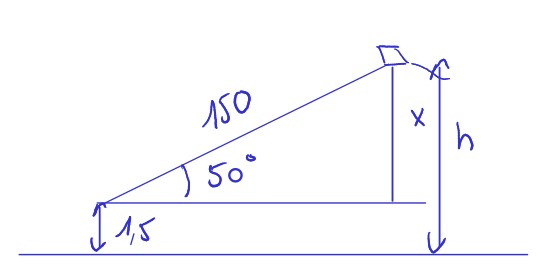
Une personne manoeuvrant un cerf-volant tient le fil à \(1.5\,m\) au-dessus du sol. Le fil du cerf-volant est tendu et forme un angle de \(50^\circ\) avec l'horizontale.
À quelle distance du sol se trouve le cerf-volant, si on laisse dérouler \(150\) mètres de fil?
Solution
\(\sin(50^\circ) = \dfrac{x}{150} \implies x = 150 \cdot \sin(50^\circ) = 114.9\,m\) \(h = 114.9 + 1.5 = 116.4\,m\) Le cerf-volant se trouve à 116.4 m du sol.
Question 6 (5 pts)#
\(ABCD\) est un rectangle. Sachant que \(\alpha = 65^\circ\) et \(\overline{EC} = 11\,cm\), calculez \(\widehat{AEB}\), ainsi que l'aire et le périmètre du triangle \(ABE\).
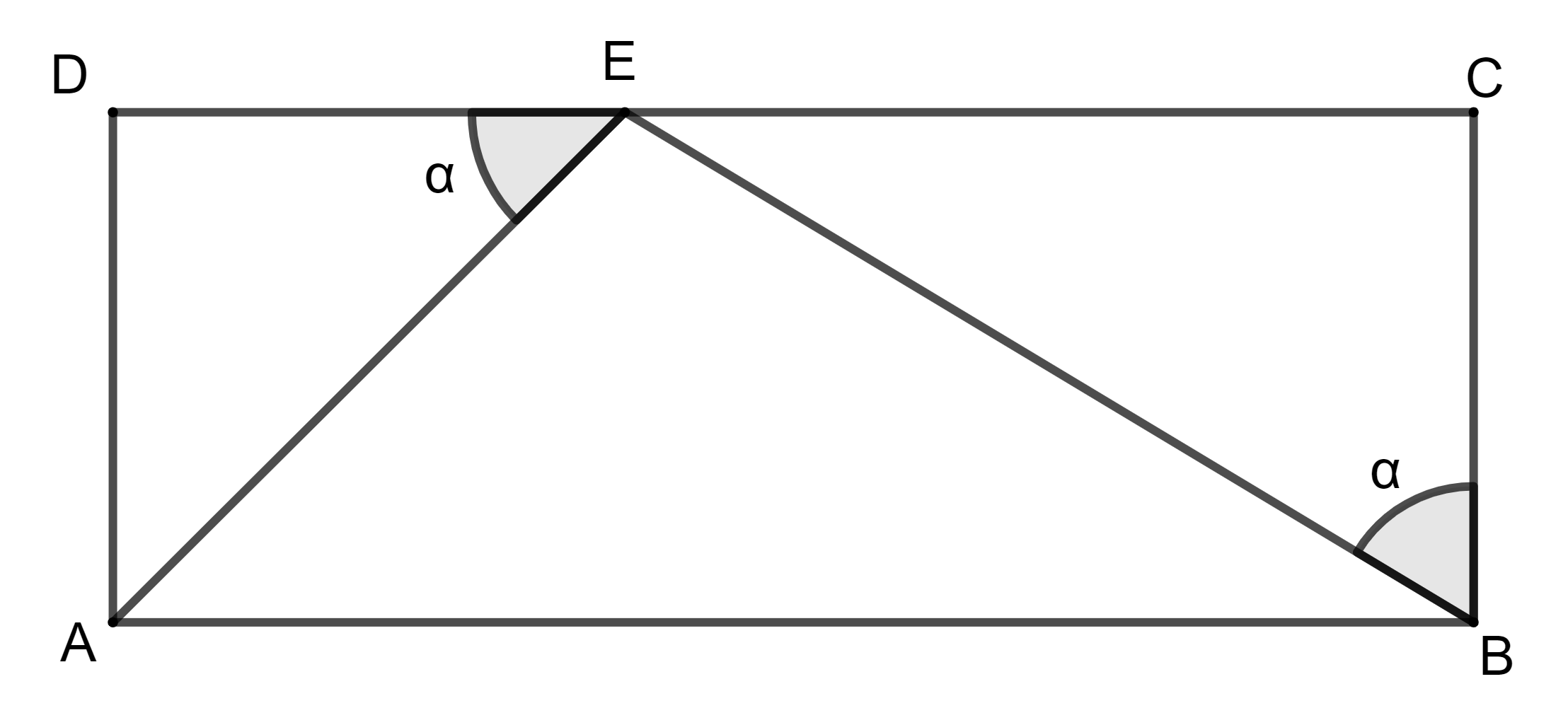
Solution
\(\widehat{BEC} = 180^\circ - 90^\circ - 65^\circ = 25^\circ\)
\(\widehat{AEB} = 180^\circ - 65^\circ - 25^\circ = 90^\circ\)
Le triangle \(AEB\) est rectangle en \(E\).
Par la trigo:
\(\sin(65^\circ) = \dfrac{11}{EB} \implies EB = \dfrac{11}{\sin(65^\circ)} = 12.1\,cm\)
Par Pythagore:
\(\overline{EH} = \sqrt{12.1^2-11^2} = 5.1\,cm\)
Par le thm de la hauteur:
\(EH^2 = AH \cdot HB\)
\(AH = \dfrac{EH^2}{HB} = \dfrac{5.1^2}{11} = 2.4\,cm\)
Par Pythagore:
\(AB = AH + HB = 2.4 + 11 = 13.4\,cm\)
\(AE = \sqrt{13.4^2 - 12.1^2} = 5.7\,cm\)
Aire:
\(A = \dfrac{13.4 \cdot 5.1}{2} = 34.3\,cm^2\)
Périmètre:
\(P = 12.1 + 13.4 + 5.7 = 31.2\,cm\)